Сообщения.

Астрономия

Астроно́мия (др.-греч. ἀστρονομία, от ἄστρον — звезда и νόμος — закон) — наука о движении, строении и развитии небесных тел и их систем, вплоть до Вселенной в целом.[1] В частности, астрономия изучает Солнце, планеты Солнечной системы и их спутники, астероиды, кометы, метеориты, межпланетное вещество, звёзды и внесолнечные планеты (экзопланеты), туманности, межзвёздное вещество, галактики и их скопления, пульсары, квазары, чёрные дыры и многое другое.

2009 год был объявлен ООН Международным годом астрономии (IYA2009). Основной упор делается на повышении общественной заинтересованности и понимании астрономии.

Структура астрономии как научной дисциплины

Лунная астрономия: большой кратер на изображении — Дедал, сфотографированный экипажем Аполлона-11 во время обращения вокруг Луны в 1969. Кратер расположен рядом с центром невидимой стороны Луны, его диаметр около 93 км.
Внегалактическая астрономия: гравитационное линзирование. Это изображение показывает несколько голубых петлеобразных объектов, которые являются многократными изображениями одной галактики, размноженными из-за эффекта гравитационной линзы от скопления жёлтых галактик возле центра фотографии. Линза создана гравитационным полем скопления, которое искривляет световые лучи, что ведёт к увеличению и искажению изображения более далёкого объекта.

Современная астрономия подразделяется на ряд отдельных разделов, которые тесно связаны между собой, и такое разделение астрономии в известном смысле условно. Главнейшими разделами астрономии являются:

  • Астрометрия — изучает видимые положения и движения светил. На этапе исторического развития науки роль астрометрии долгое время состояла также в высокоточном определении географических координат и времени с помощью изучения движения небесных светил (в данный момент для того и другого существуют новейшие способы). Современная астрометрия состоит из:
    • фундаментальной астрометрии, задачами которой являются определение координат небесных тел из наблюдений, составление каталогов звёздных положений и определение числовых значений астрономических параметров, — величин, позволяющих учитывать закономерные изменения координат светил;
    • радиоастрономии
    • сферической астрономии, разрабатывающей математические методы определения видимых положений и движений небесных тел с помощью различных систем координат, а также теорию закономерных изменений координат светил со временем;
  • Теоретическая астрономия даёт методы для определения орбит небесных тел по их видимым положениям и методы вычисления эфемерид (видимых положений) небесных тел по известным элементам их орбит (обратная задача).
  • Небесная механика изучает законы движений небесных тел под действием сил всемирного тяготения, определяет массы и форму небесных тел и устойчивость их систем.

Эти три раздела в основном решают первую задачу астрономии (исследование движения небесных тел), и их часто называют классической астрономией.

  • Астрофизика изучает строение, физические свойства и химический состав небесных объектов. Она делится на: а) практическую (наблюдательную) астрофизику, в которой разрабатываются и применяются практические методы астрофизических исследований и соответствующие инструменты и приборы; б) теоретическую астрофизику, в которой, на основании законов физики, даются объяснения наблюдаемым физическим явлениям.

Ряд разделов астрофизики выделяется по специфическим методам исследования.

  • Звёздная астрономия изучает закономерности пространственного распределения и движения звёзд, звёздных систем и межзвёздной материи с учётом их физических особенностей.

В этих двух разделах в основном решаются вопросы второй задачи астрономии (строение небесных тел).

  • Космогония рассматривает вопросы происхождения и эволюции небесных тел, в том числе и нашей Земли.
  • Космология изучает общие закономерности строения и развития Вселенной.

На основании всех полученных знаний о небесных телах последние два раздела астрономии решают её третью задачу (происхождение и эволюция небесных тел).

Курс общей астрономии содержит систематическое изложение сведений об основных методах и главнейших результатах, полученных различными разделами астрономии.

Одним из новых, сформировавшихся только во второй половине XX века, направлений является археоастрономия, которая изучает астрономические познания древних людей и помогает датировать древние сооружения, исходя из явления прецессии Земли.

 Звёздная астрономия

Планетарная туманность Муравья — Mz3. Выброс газа из умирающей центральной звезды показывает симметричную модель, в отличие от хаотических образов обычных взрывов.
Основная статья: Звезда

Изучение звёзд и звёздной эволюции имеет фундаментальное значение для нашего понимания Вселенной. Астрофизика звезд развивалась на основе наблюдений и теоретического понимания, а сейчас и с помощью компьютерного моделирования.

Формирование звезд происходит в областях плотной пыли и газа, известных как гигантские молекулярные облака. Если происходит дестабилизация, то фрагменты облака могут сжаться под воздействием гравитации и сформировать протозвезду. Достаточно плотные и горячие области вызовут термоядерные реакции, таким образом начнется главная последовательность звезды.[2]

Почти все элементы, более тяжелые чем водород и гелий, создаются внутри ядра звезды.

Задачи астрономии

Радиотелескопы среди множества различных инструментов, используемых астрономами.

Основными задачами астрономии являются:

  1. Изучение и объяснение видимых движений небесных тел, нахождение закономерностей и причин этих движений.
  2. Изучение строения небесных тел, их физических и химических свойств, построение моделей их внутреннего строения.
  3. Решение проблем происхождения и развития небесных тел и их систем.
  4. Изучение наиболее общих свойств Вселенной, построение теории наблюдаемой части Вселенной — Метагалактики.

Решение этих задач требует создания эффективных методов исследования — как теоретических, так и практических. Первая задача решается путём длительных наблюдений, начатых ещё в глубокой древности, а также на основе законов механики, известных уже около 300 лет. Поэтому в этой области астрономии мы располагаем наиболее богатой информацией, особенно для сравнительно близких к Земле небесных тел: Луны, Солнца, планет, астероидов и т. д.

Решение второй задачи стало возможным в связи с появлением спектрального анализа и фотографии. Изучение физических свойств небесных тел началось во второй половине XIX века, а основных проблем — лишь в последние годы.

Третья задача требует накопления наблюдаемого материала. В настоящее время таких данных ещё недостаточно для точного описания процесса происхождения и развития небесных тел и их систем. Поэтому знания в этой области ограничиваются только общими соображениями и рядом более или менее правдоподобных гипотез.

Четвёртая задача является самой масштабной и самой сложной. Практика показывает, что для её решения уже недостаточно существующих физических теорий. Необходимо создание более общей физической теории, способной описывать состояние вещества и физические процессы при предельных значениях плотности, температуры, давления. Для решения этой задачи требуются наблюдательные данные в областях Вселенной, находящихся на расстояниях в несколько миллиардов световых лет. Современные технические возможности не позволяют детально исследовать эти области. Тем не менее, эта задача сейчас является наиболее актуальной и успешно решается астрономами ряда стран, в том числе и России.

 История астрономии

Основная статья: История астрономии

Ещё в глубокой древности люди интересовались движением светил по небосводу, хотя астрономия тогда была основательно перемешана с астрологией. Окончательное выделение научной астрономии произошло в эпоху Возрождения и заняло долгое время.

 

понедельник, 27 сентября 2010 г.

Решения уравнений Эйнштейна для чёрных дыр

Так как чёрные дыры являются локальными и относительно компактными образованиями, то при построении их теории обычно пренебрегают наличием космологической постоянной, так как её эффекты для таких характерных размеров задачи неизмеримо малы. Тогда стационарные решения для чёрных дыр в рамках ОТО, дополненной известными материальными полями, характеризуются только тремя параметрами: массой (M), моментом импульса (L) и электрическим зарядом (Q), которые складываются из соответствующих характеристик вошедших в чёрную дыру при коллапсе и упавших в неё позднее тел и излучений (если в природе существуют магнитные монополи, то чёрные дыры могут иметь также магнитный заряд (G)[9], но пока подобные частицы не обнаружены). Любая чёрная дыра стремится в отсутствие внешних воздействий стать стационарной, что было доказано усилиями многих физиков-теоретиков, из которых особо следует отметить вклад нобелевского лауреата Субраманьяна Чандрасекара, перу которого принадлежит фундаментальная для этого направления монография «Математическая теория чёрных дыр»[10]. Более того, представляется, что никаких других характеристик, кроме этих трёх, у не возмущаемой снаружи чёрной дыры быть не может, что формулируется в образной фразе Уилера как: «Чёрные дыры не имеют волос»[9].
Решения уравнений Эйнштейна для чёрных дыр с соответствующими характеристиками:
Характеристика ЧД Без вращения Вращается
Без заряда Решение Шварцшильда Решение Керра
Заряженная Решение Райсснера — Нордстрёма Решение Керра — Ньюмена
  • Решение Шварцшильда (1916 год, Карл Шварцшильд) — статичное решение для сферически-симметричной чёрной дыры без вращения и без электрического заряда.
  • Решение Райсснера — Нордстрёма (1916 год, Ханс Райсснер (нем.) и 1918 год, Гуннар Нордстрём (англ.)) — статичное решение сферически-симметричной чёрной дыры с зарядом, но без вращения.
  • Решение Керра (1963 год, Рой Керр (англ.)) — стационарное, осесимметричное решение для вращающейся чёрной дыры, но без заряда.
  • Решение Керра — Ньюмена (1965 год, Э. Т. Ньюмен (англ.), Э. Кауч, К. Чиннапаред, Э. Экстон, Э. Пракаш и Р. Торренс)[11] — наиболее полное на данный момент решение: стационарное и осесимметричное, зависит от всех трёх параметров.
Решение для вращающейся чёрной дыры чрезвычайно сложно. Его вывод был описан Керром в 1963 году очень кратко[12], и лишь спустя год детали были опубликованы Керром и Шильдом в малоизвестных трудах конференции. Подробное изложение вывода решений Керра и Керра — Ньюмена было опубликовано в 1969 году в известной работе Дебнея, Керра и Шильда[13]. Последовательный вывод решения Керра был также проделан Чандрасекаром более чем на пятнадцать лет позже[10].
Считается, что наибольшее значение для астрофизики имеет решение Керра, так как заряженные чёрные дыры должны быстро терять заряд, притягивая и поглощая противоположно заряженные ионы и пыль из космического пространства. Существует также теория[14], связывающая гамма-всплески с процессом взрывной нейтрализации заряженных чёрных дыр путём рождения из вакуума электрон-позитронных пар (Р. Руффини с сотрудниками), но она оспаривается рядом учёных[15].

 Теоремы об «отсутствии волос»

Теоремы об «отсутствии волос» у чёрной дыры (англ. No hair theorem) говорят о том, что у стационарной чёрной дыры внешних характеристик, помимо массы, момента импульса и определённых зарядов (специфических для различных материальных полей), быть не может, и детальная информация о материи будет потеряна (и частично излучена вовне) при коллапсе. Большой вклад в доказательство подобных теорем для различных систем физических полей внесли Брэндон Картер, Вернер Израэль, Роджер Пенроуз, Пётр Крушель (Chruściel), Маркус Хойслер. Сейчас представляется, что данная теорема верна для известных в настоящее время полей, хотя в некоторых экзотических случаях, аналогов которых в природе не обнаружено, она нарушается[16].

[править] Решение Шварцшильда

Основная статья: Метрика Шварцшильда

 Основные свойства


Рисунок художника: аккреционный диск горячей плазмы, вращающийся вокруг чёрной дыры.
Согласно теореме Биркхофа, гравитационное поле любого сферически симметричного распределения материи вне её даётся решением Шварцшильда. Поэтому слабо вращающиеся чёрные дыры, как и пространство-время вблизи Солнца и Земли, в первом приближении тоже описываются этим решением.
Две важнейшие черты, присущие чёрным дырам в модели Шварцшильда — это наличие горизонта событий (он по определению есть у любой чёрной дыры) и сингулярности, которая отделена этим горизонтом от остальной Вселенной.
Решением Шварцшильда точно описывается изолированная невращающаяся, незаряженная и не испаряющаяся чёрная дыра (это сферически симметричное решение уравнений гравитационного поля (уравнений Эйнштейна) в вакууме). Её горизонт событий — это сфера, радиус которой, определённый из её площади по формуле S = 4πr2, называется гравитационным радиусом или радиусом Шварцшильда.
Все характеристики решения Шварцшильда однозначно определяются одним параметром — массой. Так, гравитационный радиус чёрной дыры массы M равен[17]
r_s = {2\,GM \over c^2},
где G — гравитационная постоянная, а c — скорость света. Чёрная дыра с массой, равной массе Земли, обладала бы радиусом Шварцшильда в 9 мм (то есть Земля могла бы стать чёрной дырой, если бы кто-либо смог сжать её до такого размера). Для Солнца радиус Шварцшильда составляет примерно 3 км.
Объекты, размер которых наиболее близок к своему радиусу Шварцшильда, но которые ещё не являются чёрными дырами, — это нейтронные звёзды.
Можно ввести понятие «средней плотности» чёрной дыры, поделив её массу на «объём, заключённый под горизонтом событий»[18]:
\rho=\frac{3\,c^6}{32\pi M^2G^3}.
Средняя плотность падает с ростом массы чёрной дыры. Так, если чёрная дыра с массой порядка солнечной обладает плотностью, превышающей ядерную плотность, то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр подозревается в квазарах) обладает средней плотностью порядка 20 кг/м³, что существенно меньше плотности воды. Таким образом, чёрную дыру можно получить не только сжатием имеющегося объёма вещества, но и экстенсивным путём, накоплением огромного количества материала.
Для более точного описания реальных чёрных дыр необходим учёт наличия момента импульса. Кроме того, малые, но концептуально важные добавки для чёрных дыр астрофизических масс — излучение Старобинского и Зельдовича и излучение Хокинга — следуют из квантовых поправок[19]. Учитывающую это теорию (то есть ОТО, в которой правая часть уравнений Эйнштейна есть среднее по квантовому состоянию от тензора энергии-импульса) обычно называют «полуклассической гравитацией». Представляется, что для очень малых чёрных дыр эти квантовые поправки должны стать определяющими, однако это точно не известно, так как отсутствует непротиворечивая модель квантовой гравитации.

 Метрическое описание и аналитическое продолжение

В 1915 году К. Шварцшильд выписал решения уравнений Эйнштейна для пустого пространства в сферически симметричном статическом случае (позднее Биркхоф показал, что последнее предположение излишне[20]). Это решение оказалось пространством-временем \mathcal M с топологией R^2\times S^2 и интервалом, приводимым к виду
ds^2 =-(1-r_s/r)c^2d t^2 + (1-r_s/r)^{-1}d r^2 + r^2(d \theta^2+\sin^2\theta\, d\varphi^2),
где
t — временная координата, в секундах,
r — радиальная координата, в метрах,
θ — географическая широта (угол от севера), в радианах,
\varphi — долгота, в радианах,
rs — радиус Шварцшильда тела с массой M, в метрах.

Геометрический смысл ~r состоит в том, что площадь поверхности сферы \{(t,r,\theta,\varphi)\mid t=t_0,\ r=r_0\} есть ~4\pi r_0^2. Важно, что координата ~r принимает только значения, большие ~r_s , а значение параметра ~r , в отличие от лапласовского случая, не является «расстоянием до центра», так как центра как точки (события на действительной мировой линии какого-либо тела) в шварцшильдовском пространстве \mathcal M вообще нет.
Наконец, угловые координаты θ и \varphi соответствуют сферической симметрии задачи и связаны с её 3 векторами Киллинга.
Из основных принципов ОТО следует, что такую метрику создаст (снаружи от себя) любое сферически симметричное тело с радиусом ~>r_s и массой M = {c^2r_s\over 2G } , где G — гравитационная постоянная, а c — скорость света. Замечательно, хотя и в некоторой степени случайно, что величина гравитационного радиуса — радиус Шварцшильда \,r_s  — совпадает с гравитационным радиусом \,r_g, вычисленным ранее Лапласом для тела массы ~M .
Как видно из приведённой формы метрики, коэффициенты при t и r ведут себя патологически при r\rightarrow r_s , где и располагается горизонт событий чёрной дыры Шварцшильда. Эти патологии являются, однако, лишь эффектом выбора координат (подобно тому, как в сферической системе координат при θ = 0 любое значение \varphi описывает одну и ту же точку). Пространство Шварцшильда \mathcal M можно, как говорят, «продолжить за горизонт», и если там тоже считать пространство везде пустым, то при этом возникает большее пространство-время \tilde{\mathcal M} , которое называется обычно максимально продолженным пространством Шварцшильда или (реже) пространством Крускала.
Рис. 1. Сечение ~\theta=\mathrm{const},\ \varphi=\mathrm{const} пространства Шварцшильда. Каждой точке на рисунке соответствует сфера площадью ~4\pi r^2(u,v). Радиальные светоподобные геодезические (то есть мировые линии фотонов) — это прямые под углом ~45^\circ к вертикали, иначе говоря — это прямые ~u=\mathrm{const} или ~v=\mathrm{const}
Интервал этого пространства \tilde{\mathcal M} имеет вид
ds^2 =-F(u,v)^2 \,du\,dv+r^2(u,v)(d \theta^2+\sin^2\theta\, d\varphi^2),
где \,F=\frac{4 r_s^3}{r}e^{-r/r_s}, а функция ~r(u,v) определяется (неявно) уравнением ~(1-r/r_s)e^{r/r_s}=uv . Пространство \tilde{\mathcal M} максимально, то есть его уже нельзя изометрически вложить в большее пространство-время (его нельзя «продолжить»). Исходное пространство \mathcal M является всего лишь частью \tilde{\mathcal M} при v>0,\ r>r_s — область I на рисунке. Тело, движущееся медленнее света — мировая линия такого тела будет кривой с углом наклона к вертикали меньше ~45^\circ, см. кривую ~\gamma на рисунке — может покинуть \mathcal M . При этом оно попадает в область II, где ~r<r_s. Покинуть эту область и вернуться к ~r>r_s оно, как видно из рисунка, уже не сможет (для этого пришлось бы отклониться более, чем на ~45^\circ от вертикали, то есть превысить скорость света). Область II, таким образом, представляет собой чёрную дыру. Её граница (ломаная, v\geqslant 0,\ r=r_s) соответственно является горизонтом событий.
Отметим несколько замечательных свойств максимально продолженного Шварцшильдовского пространства ~\tilde{\mathcal M} :
  1. Оно сингулярно: координата ~r наблюдателя, падающего под гоpизонт, уменьшается и стремится к нулю, когда его собственное время ~\tau стремится к некоторому конечному значению ~\tau_0. Однако его мировую линию нельзя продолжить в область \tau \geqslant\tau_0 , так как точек с ~r=0 в этом пространстве нет. Таким образом, судьба наблюдателя нам известна только до некоторого момента его (собственного) времени;
  2. Хотя пространство \mathcal M статично (видно, что метрика (1) не зависит от времени), пространство \tilde{\mathcal M} таковым не является.
  3. Область III тоже изометрична \mathcal M . Таким образом, пространство Шварцшильда содержит две «вселенные» — «нашу» (это \mathcal M ) и ещё одну такую же. Область II внутри чёрной дыры, соединяющая их, называется мостом Эйнштейна — Розена. Попасть во вторую вселенную наблюдатель, стартовавший из I и движущийся медленнее света, не сможет (см. рис. 1), однако в промежуток времени между пересечением горизонта и попаданием на сингулярность он сможет увидеть её. Такая структура пространства-времени, которая сохраняется и даже усложняется при рассмотрении более сложных чёрных дыр, породила многочисленные спекуляции на тему возможных параллельных вселенных и путешествий в них через чёрные дыры как в научной литературе, так и в научно-фантастической (см. Кротовые норы).
Рис. 2. Сечения пространства Шварцшильда в разные моменты времени (одно измерение опущено)
Чтобы представить себе структуру 4-мерного пространства-времени ~\tilde{\mathcal M}, его удобно условно рассматривать как эволюцию 3-мерного пространства. Для этого можно ввести «временную» координату ~T=(u+v)/2 и сечения ~T=const (это пространственно-подобные поверхности, или «поверхности одновременности») воспринимать как ~\tilde{\mathcal M} «в данный момент времени». На рис. 2 показаны такие сечения для разных моментов ~T. 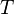Мы видим, что вначале имеются два несвязанных 3-мерных пространства. Каждое из них сферически симметрично и асимптотически плоско. Точка ~r=0 отсутствует и при ~r\to 0 кривизна неограниченно растёт (сингулярность). В момент времени ~T=-1 обе сингулярности исчезают и между ранее не связанными пространствами возникает «перемычка» (в современной терминологии кротовая нора). Радиус её горловины возрастает до ~r_s при ~T=0, затем начинает уменьшаться и при ~T=1 перемычка снова разрывается, оставляя два пространства несвязанными.

 Решение Райсснера — Нордстрёма

Это статичное решение (не зависящее от временной координаты) уравнений Эйнштейна для сферически-симметричной чёрной дыры с зарядом, но без вращения.
Метрика чёрной дыры Райсснера — Нордстрёма:
{d s}^{2} = -\left( 1 - \frac{r_{s}}{r} + \frac{r_{Q}^{2}}{r^{2}} \right) c^{2} dt^{2} + \frac{dr^{2}}{\displaystyle{1 - \frac{r_{s}}{r} + \frac{r_{Q}^{2}}{r^{2}}}} + r^{2}( d\theta^{2} + \sin^{2} \theta \, d\varphi^{2}),
где
c — скорость света, м/с,
t — временная координата (время, измеряемое на бесконечно удалённых неподвижных часах), в секундах,
r — радиальная координата (длина «экватора» изометрической сферы[21], делённая на 2π), в метрах,
θ — географическая широта (угол от севера), в радианах,
\varphi — долгота, в радианах,
rs — радиус Шварцшильда (в метрах) тела с массой M,
rQ — масштаб длины (в метрах), соответствующий электрическому заряду Q (аналог радиуса Шварцшильда, только не для массы, а для заряда) определяемый как
r_{Q}^{2} = \frac{Q^{2}G}{4\pi\varepsilon_{0} c^{4}},
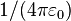где 1/(4\pi\varepsilon_0) — это постоянная Кулона.
Параметры чёрной дыры не могут быть произвольными. Максимальный заряд, который может иметь ЧД Райсснера — Нордстрёма, равен Q_{max} = M \approx 10^{40} e \, M/M_{\odot}, где e — заряд электрона. Это частный случай ограничения Керра — Ньюмена для ЧД с нулевым угловым моментом (J = 0, то есть без вращения). При превышении этого критического заряда формально решение уравнений Эйнштейна существует, но «собрать» такое решение из внешнего заряженного вещества не получится: гравитационное притяжение не сможет компенсировать собственное электрическое отталкивание материи (см.: Принцип космической цензуры). Кроме того, надо заметить, что в реалистичных ситуациях чёрные дыры не должны быть сколь-либо значительно заряжены.

 Решение Керра

Чёрная дыра Керра обладает рядом замечательных свойств. Вокруг горизонта событий существует область, называемая эргосферой, внутри которой телам невозможно покоиться относительно удалённых наблюдателей. Они могут только вращаться вокруг чёрной дыры по направлению её вращения[22]. Этот эффект называется «увлечением инерциальной системы отсчёта» (англ.  frame-dragging) и наблюдается вокруг любого вращающегося массивного тела, например, вокруг Земли или Солнца, но в гораздо меньшей степени. Однако саму эргосферу ещё можно покинуть, эта область не является захватывающей. Размеры эргосферы зависят от углового момента вращения.
Параметры чёрной дыры не могут быть произвольными (см.: Принцип космической цензуры). При Jmax = M2 метрика называется предельным решением Керра. Это частный случай ограничения Керра — Ньюмена, для ЧД с нулевым зарядом (Q = 0).
Это и другие решения типа «чёрная дыра» порождают удивительную геометрию пространства-времени. Однако требуется анализ устойчивости соответствующей конфигурации, которая может быть нарушена за счёт взаимодействия с квантовыми полями и других эффектов.
Для пространства-времени Керра анализ был проведён Субраманьяном Чандрасекаром и другими физиками и было обнаружено, что керровская чёрная дыра — а точнее её внешняя область — является устойчивой[10]. Аналогично, как частные случаи, оказались устойчивыми шварцшильдовские и рейсснер-нордстрёмовские дыры.

 Решение Керра — Ньюмена

Трёхпараметрическое семейство Керра — Ньюмена — наиболее общее решение, соответствующее конечному состоянию равновесия не возмущаемой внешними полями чёрной дыры (согласно теоремам об «отсутствии волос» для известных физических полей). В координатах Бойера — Линдквиста (Boyer — Lindquist) метрика Керра — Ньюмена даётся выражением:
ds^2 = -\left(1-{2\,Mr\over\Sigma}\right)\,dt^2-4Mra{\sin^2\theta\over\Sigma}\,dt\,d\varphi\,+
+\left(r^2+a^2+{2\,Mra^2\sin^2\theta\over\Sigma}\right)\sin^2\theta\,{d\varphi^2}+{\Sigma\over\Delta}\,dr^2+{\Sigma\,{d\theta^2}},
где \Sigma \equiv r^2 + a^2 \cos^2\theta; \Delta \equiv r^2 - 2 Mr + a^2 + Q^2 и a \equiv J/M.
Из этой простой формулы легко вытекает, что горизонт событий находится на радиусе: r_+ = M + \sqrt{M^2 - Q^2 - a^2}, и следовательно параметры чёрной дыры не могут быть произвольными: электрический заряд и угловой момент не могут быть больше значений, соответствующих исчезновению горизонта событий. Должны выполняться следующие ограничения:
a^2 + Q^2 \leqslant M^2 — это ограничение для ЧД Керра — Ньюмена.
Если эти ограничения нарушатся, горизонт событий исчезнет, и решение вместо чёрной дыры будет описывать так называемую «голую» сингулярность, но такие объекты, согласно распространённым убеждениям, в реальной Вселенной существовать не должны (согласно пока не доказанному, но правдоподобному принципу космической цензуры). Альтернативно, под горизонтом может находиться источник сколлапсировавшей материи, которая закрывает сингулярность, и поэтому внешнее решение Керра или Керра-Ньюмена должно быть непрерывно состыковано с внутренним решением уравнений Эйнштейна с тензором энергии-импульса этой материи. Сингулярность исчезает вместе с ограничением на параметры ЧД решения Керра-Ньюмена.
Наиболее простое выражение решения Керра и Керра — Ньюмена принимают в форме Керра — Шильда (КШ)[13], в которой метрика имеет вид
gμν = ημν + 2Hkμkν,
где ημν является метрикой вспомогательного пространства Минковского с декартовыми координатами x = xμ(x) = (t,x,y,z).
В этой форме kμ(x) является векторным полем световых направлений. Часто говорят "нулевых" направлений, поскольку kμkμ = gμνkμkν = 0. Заметим, что специфическая структура формы метрики КШ гарантирует, что поле kμ(x) является также нулевым относительно вспомогательного плоского пространства, т.е. ημνkμkν = 0 .
Функция H имеет вид
H =\frac {Mr - |Q|^2/2} {r^2+ a^2 \cos^2\theta} ,
где r,θ - это сплюснутые сфероидальные координаты Керра, которые определяются соотношением
x+iy = (r + ia) e^{i\phi} \sin \theta , \ z=r\cos \theta .
и переходят вдали от ЧД в обычные сферические координаты. В этих координатах компоненты вектора kα определяются из дифференциальной формы
kαdxα = dr − dt − asin2θdφ
путём сравнения коэффициетов перед дифференциалами. Это один из примеров вычисления с применением очень удобного аппарата внешних форм, который и был использован Керром для получения решения в первой и последующих работах.
В действительности, Керровская угловая координата φ очень необычна, и простая форма КШ связана с тем, что вся сложность решения скрыта в форме векторного поля kμ(x) , которая представляет собой вихревой поток светового излучения образующий так называемую Главную Нулевую Конгруэнцию (ГНК). В декартовых координатах компоненты векторного поля kμ определяются формой
k_\mu dx^\mu = - dt +\frac z r dz + \frac r {r^2 +a^2} (xdx+ydy) - \frac a {r^2 +a^2} (xdy-ydx) .
В теории КШ, для определения этого поля используются также "нулевые" (световые) декартовы координаты
u=(z-t)/\sqrt {2},\quad v=(z+t)/\sqrt {2},\quad \zeta=(x+iy)/\sqrt {2},\quad \bar\zeta=(x-iy)/\sqrt {2} ,
в которых конгруэнция имеет компоненты, определяемые дифференциальной формой
k_\mu^{(\pm)} dx^\mu = P^{-1}(du +\bar Y^\pm d\zeta + Y^\pm d\bar\zeta - Y^\pm \bar Y^{(\pm)} dv) .
Это выражение определяется комплексной функцией Y(x), которая имеет два решения Y^\pm (x) , что даёт для векторного поля kμ(x) две различные конгруэнции (ГНК). Таким образом, решение для вращающихся ЧД может быть записано в двух различных формах, которые базируются на "входящей в" ЧД или "исходящей из" ЧД конгруэнции, что соответствует так-называемым алгебраически специальным решениям типа D.
Представление в форме КШ обладает рядом преимуществ, т. к. конгруэнция, все координаты и форма решений для электромагнитного (ЭМ) поля и метрики оказываются жёстко связанными с координатами вспомогательного плоского пространства и не зависят от положения горизонта и границы эргосферы. Более того, решения КШ однозначно продолжаются аналитически через горизонт внутрь ЧД и далее на "отрицательный" лист, область отрицательных значений сплюснутой радиальной координаты r.
В координатах Керра θ,φ функция Y(x) имеет вид
Y(x) = e^{i\phi} \tan \frac \theta 2 .
Геометрически, она представляет собой проекцию небесной сферы с координатами θ,φ на комплексную плоскость Y , однако зависимость x \to Y(x) очень нетривиальна и задаётся тесно связанной с твисторами Теоремой Керра. Фактически, ГНК формирует костяк решения Керра как вихрь твисторных лучей. Функция P для покоящегося решения имеет вид
P = \frac 1 {\sqrt 2} (1+ Y \bar Y ) .
Подобно форме метрики КШ, все тензорные характеристики решения должны быть согласованными (aligned) с векторным полем ГНК, и в частности, вектор-потенциал ЭМ поля решения Керра — Ньюмена выражается в виде
A^\mu = \Re e \frac {Q r}{r^2 + a^2 \cos ^2 \theta} k^\mu .
Керровская сингулярность находится под горизонтом. Она связана с сингулярностью функции H и соответствует значениям r = 0 и одновременно θ = 0. Она представляет собой кольцо, открывающее проход к отрицательному листу геометрии Керра, r < 0, на котором значения массы и заряда, а также направления полей меняются на обратные. (Не путайте с максимальным аналитическим расширением решений через горизонт ЧД описанным несколько ниже.) Этот второй лист ("Алисово зазеркалье") долгое время был загадкой решения Керра.
Ещё в 1970 году В. Израэль рассмотрел источник решения Керра — Ньюмена в виде вращающегося диска, закрывающего этот ход. Это направление было развито К. Лопезом (C. L`opez), показавшим, что керровская сингулярность может быть закрыта вращающейся оболочкой (bubble), и в этом случае ограничение на параметры решения Керра — Ньюмена не действует. Более того, как заметил Б. Картер (1968), решение Керра — Ньюмена с большим угловым моментом обладает двойным гиромагнитным отношением, таким же, как у электрона согласно уравнению Дирака. История этого направления для решения Керра — Ньюмена излагается в работе arXiv:0910.5388[hep-th].
Метрику Керра — Ньюмена (и просто Керра, но не Шварцшильда) можно аналитически продолжить также через гороизонт таким образом, чтобы соединить в чёрной дыре бесконечно много «независимых» пространств. Это могут быть как «другие» вселенные, так и удалённые части нашей Вселенной. В таким образом полученных пространствах есть замкнутые времениподобные кривые: путешественник может, в принципе, попасть в своё прошлое, то есть встретиться с самим собой. Вокруг горизонта событий вращающейся чёрной дыры также существует область, называемая эргосферой, практически эквивалентная эргосфере из решения Керра; находящийся там стационарный наблюдатель обязан вращаться с положительной угловой скоростью (в сторону вращения чёрной дыры).
Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)